Population Size Estimation with Many Lists and Heterogeneity: A Conditional Log-Linear Model Among the Unobserved

Estimated number of casualties in the Peruvian internal conflict for different identification strategies vs. positivity lower bound on the estimated q-probabilities.

Abstract

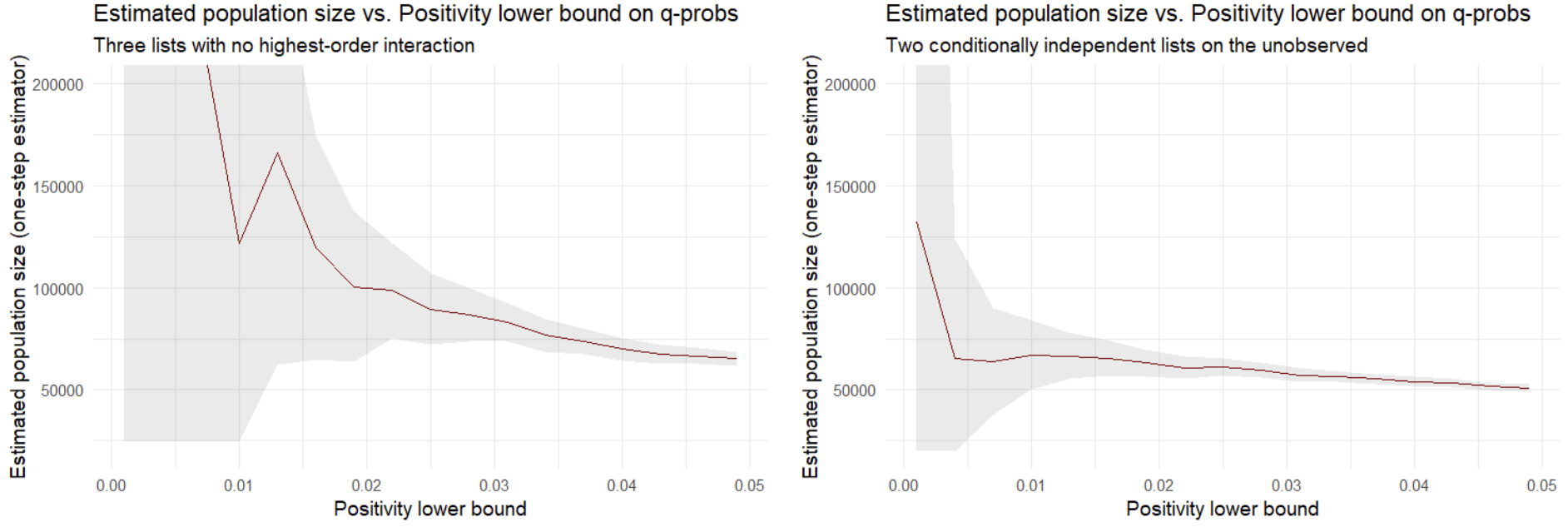
We contribute a general and flexible framework to estimate the size of a closed population in the presence of K capture-recapture lists and heterogeneous capture probabilities. Our novel identifying strategy leverages the fact that it is sufficient for identification that a subset of the K lists are not arbitrarily dependent within the subset of the population unobserved by the remaining lists, conditional on covariates. This identification approach is interpretable and actionable, interpolating between the two predominant approaches in the literature as special cases: (conditional) independence across lists and log-linear models with no highest-order interaction. We derive nonparametric doubly-robust estimators for the resulting identification expression that are nearly optimal and approximately normal for any finite sample size, even when the heterogeneous capture probabilities are estimated nonparametrically using machine learning methods. Additionally, we devise a sensitivity analysis to show how deviations from the identification assumptions affect the resulting population size estimates, allowing for the integration of domain-specific knowledge into the identification and estimation processes more transparently. We empirically demonstrate the advantages of our method using both synthetic data and real data from the Peruvian internal armed conflict to estimate the number of casualties. The proposed methodology addresses recent critiques of capture-recapture models by allowing for a weaker and more interpretable identifying assumption and accommodating complex heterogeneous capture probabilities depending on high-dimensional or continuous covariates.

Reference

Population Size Estimation with Many Lists and Heterogeneity: A Conditional Log-Linear Model Among the Unobserved
Mateo Dulce Rubio, Edward H. Kennedy
arXiv:2407.03539 (under revision) (preprint). 2024.
PDF