Conformal Mixed-Integer Constraint Learning with Feasibility Guarantees

Daniel Ovalle, Lorenz T. Biegler, Ignacio E. Grossmann, Carl D. Laird, Mateo Dulce Rubio

Empirical ground-truth feasibility rate of optimal solution across Mixed-Integer Constraint Learning (MICL) methods. Our Conformal-MICL approach (rightmost bar) is the only method that consistently satisfies the target ground-truth feasibility rate >= 90.

Abstract

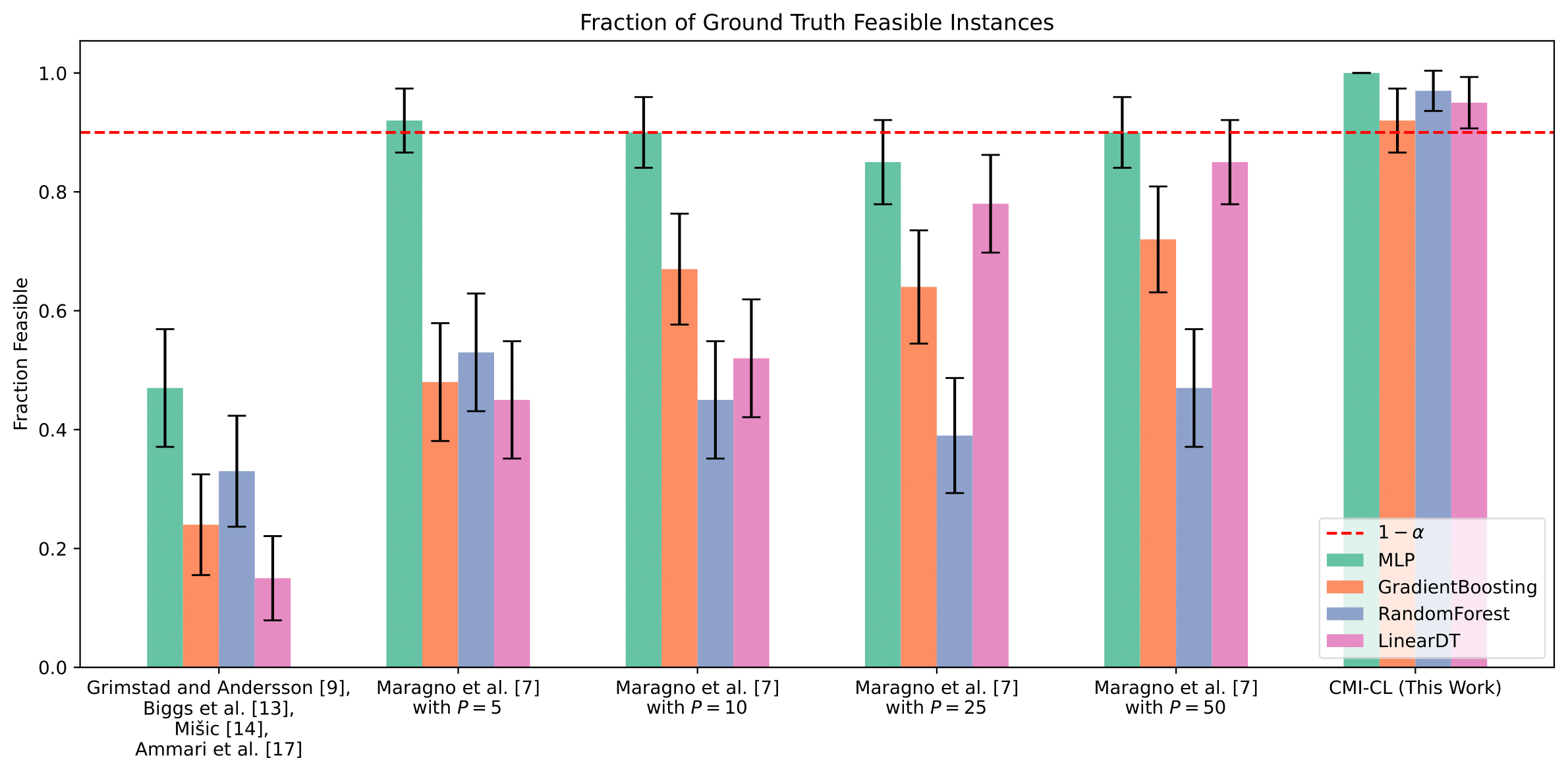
We propose Conformal Mixed-Integer Constraint Learning (C-MICL), a novel framework that provides probabilistic feasibility guarantees for data-driven constraints in optimization problems. While standard Mixed-Integer Constraint Learning methods often violate the true constraints due to model error or data limitations, our C-MICL approach leverages conformal prediction to ensure feasible solutions are ground-truth feasible. This guarantee holds with probability at least 1−α, under a conditional independence assumption. The proposed framework supports both regression and classification tasks without requiring access to the true constraint function, while avoiding the scalability issues associated with ensemble-based heuristics. Experiments on real-world applications demonstrate that C-MICL consistently achieves target feasibility rates, maintains competitive objective performance, and significantly reduces computational cost compared to existing methods. Our work bridges mathematical optimization and machine learning, offering a principled approach to incorporate uncertainty-aware constraints into decision-making with rigorous statistical guarantees.

Reference

Conformal Mixed-Integer Constraint Learning with Feasibility Guarantees
Daniel Ovalle, Lorenz T. Biegler, Ignacio E. Grossmann, Carl D. Laird, Mateo Dulce Rubio
Neural Information Processing Systems (NeurIPS (spotlight!),). 2025.
PDF